文章主题：
666AI工具大全，助力做AI时代先行者！
欢迎关注“计算机视觉研究院”
计算机视觉研究院专栏
作者：Edison_G
如同物理大时代寻求统一的量子力学，深度学习也许也需要一个统一的理论框架。
MIT 教授 Tomaso Poggio 曾在他的系列研究中 [1] 表示深度学习理论研究可以分为三大类：
表征问题（Representation）：为什么深层网络比浅层网络的表达能力更好？
最优化问题（Optimization）：为什么梯度下降能找到很好的极小值解，好的极小值有什么特点？
泛化问题（Generalization）：为什么过参数化仍然能拥有比较好的泛化性，不过拟合？
19 年顶会关于理论的研究
统计数据可见附录A：https://www.jiqizhixin.com/articles/2020-01-01-20。一般偏算法或模型的论文，阅读起来还是非常友好的，论文会介绍直观想法、形式化过程及最终结果。但偏理论的论文会要求很多领域知识，尤其是坚实的数学基础。文章后面会具体介绍几项代表性研究，但现在，我们还是先看看整体都是什么样的。
有问题的泛化性
论文 [2] 一作 Vaishnavh Nagarajan 说：「之前的研究大多数都基于一致性收敛考虑泛化边界，但我们的研究表明这类问题很可能是局限的。」目前 Rademacher Complexity、Covering Numbers 和 PAC-Bayes 等众多前沿泛化边界分析都可能存在问题。
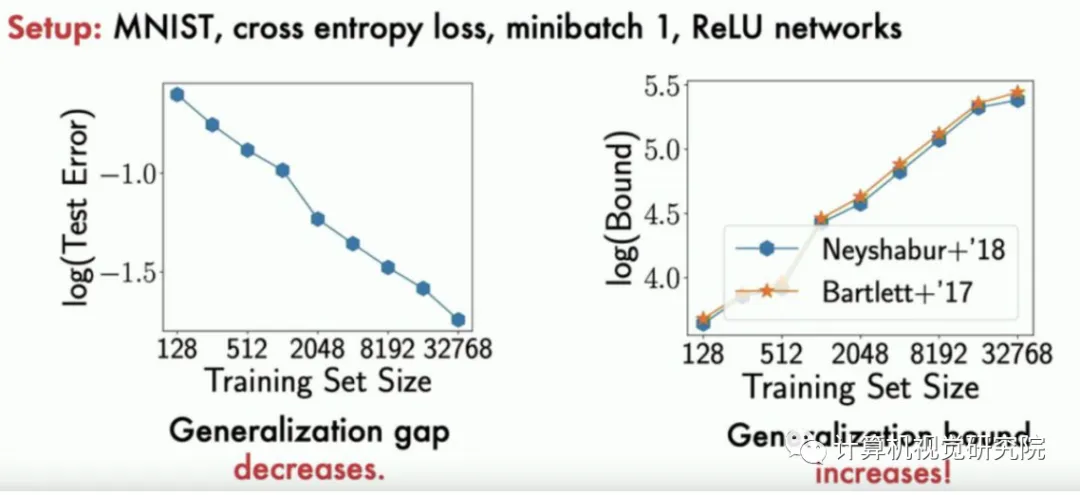
正如上式所示，即使再精炼，一致性收敛边界可能推导出约等于 1，但真实的泛化差距可能接近于 0。这样的结果是非常虚的，它并起不到什么作用。
 fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
VGG-19 在 CIFAR-10 上的测试效果，从左到右分别是迭代 30K、60K、112K 的结果。选自：arXiv:1803.03635。
参考文献：[1]Theoretical Issues in Deep Networks: Approximation, Optimization and Generalization, arXiv:1908.09375[2]Uniform convergence may be unable to explain generalization in deep learning, arXiv:1902.04742[3]The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks, arXiv:1803.03635[4]Rates of Convergence for Sparse Variational Gaussian Process Regression, arXiv:1903.03571[5]Neural Ordinary Differential Equations, arXiv:1806.07366[6]Solving Imperfect-Information Games via Discounted Regret Minimization, arXiv:1809.04040[7]Nonparametric density estimation & convergence of GANs under Besov IPM losses, arXiv:1902.03511[8]A Simple Theoretical Model of Importance for Summarization, arXiv:1801.08991[9]Density estimation by wavelet thresholding, David L Donoho et al.
© THE END
我们开创“计算机视觉协会”知识星球一年有余，也得到很多同学的认可，我们定时会推送实践型内容与大家分享，在星球里的同学可以随时提问，随时提需求，我们都会及时给予回复及给出对应的答复。
如果想加入我们“计算机视觉研究院”，请扫二维码加入我们。我们会按照你的需求将你拉入对应的学习群！计算机视觉研究院主要涉及深度学习领域，主要致力于人脸检测、人脸识别，多目标检测、目标跟踪、图像分割等研究方向。研究院接下来会不断分享最新的论文算法新框架，我们这次改革不同点就是，我们要着重”研究“。之后我们会针对相应领域分享实践过程，让大家真正体会摆脱理论的真实场景，培养爱动手编程爱动脑思考的习惯！计算机视觉研究院长按扫描二维码关注我们
AI时代，拥有个人微信机器人AI助手！AI时代不落人后！
免费ChatGPT问答，办公、写作、生活好得力助手！
搜索微信号aigc666aigc999或上边扫码，即可拥有个人AI助手！
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
