文章主题:
内容来源:新东方教育服务官微
我们的孩子会被AI取代吗?这是悬在很多家长头上的达摩克里斯之剑。
这个问题很难给出一个定论,不过从数学方面,我们今天在3.14国际π日、也是国际数学日这一天,或许能给出一个新的思考角度。
ChatGPT很强大,虽然让ChatGPT做一道小学数学题,它给出的却是错误答案:

但天才数学家陶哲轩(31岁获“数学界奥斯卡”菲尔茨奖)宣布:ChatGPT已经加入他的数学工作流,成为他的研究助手了。
各种ChatGPT的“隐藏功能”都被他挖了出来:大到寻找公式、辅助证明定理;小到改写论文语句、查询小语种数学名词的发音。
为何在普通人眼里,ChatGPT可能是个“数学菜鸡”,有些简单的问题都能答错,但陶哲轩却不这样看?
他用自己的老本行数学对AI做了个类比:
传统的计算机软件就像是数学中的标准函数,比较死板;AI工具更像是数学中的概率函数,会更加灵活。所以对做学术研究的人来说,ChatGPT是个发散思维的好工具。

他还拿ChatGPT做了一项实验,用ChatGPT求解数学题,比如该如何证明有无穷多个素数?
虽然ChatGPT给出的证明,是意料中的不完全正确,但他发现ChatGPT给出的论证思路他之前还从未见过,直接打开了他的思路。
连天才数学家都如此赞誉ChatGPT,我们又一次感受到了它的强大。
不过强大如ChatGPT,它的本质也不过是一个数学定理——贝叶斯定理,离了它,ChatGPT的智商将为零。
01
一个定理足以改变世界
贝叶斯定理,简单优雅,深刻隽永。
多数人第一次听说它,应该是在中学课堂上。公式看起来并不复杂,在一众难点考点中显得平平无奇。
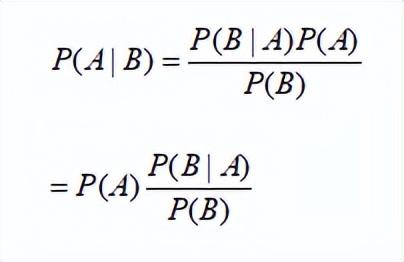
但从高校教材到研究实战,贝叶斯这三个字频繁地出现在信息科学的重要议题中。
英国靠它破译了二战德军的密码,人工智能更是靠它实现飞跃,它甚至从一个定理变成了一种思想。
我们先来简单地解释下这个公式:
P(A|B)是在B发生的情况下A发生的概率,也叫作A的后验概率,是在B事件发生之后,对A事件概率的重新评估。
P(A)是A发生的概率,也叫作A的先验概率,是在B事件发生之前,对A事件概率的一个判断。
P(B|A)是在A发生的情况下B发生的概率。
P(B)是B发生的概率。
这个公式理解起来很简单:在A发生的情况下B发生的概率*A发生的概率,指的是A、B同时发生的概率,在B发生的情况下A发生的概率*B发生的概率,指的也是A、B同时发生的概率,所以这个公式自然成立。
公式看起来简单,但它的本质并不简单,贝叶斯公式其实指向的是“逆向概率”。

什么是“逆向概率”?
假设袋子里面有P只红球,Q只白球,它们除了颜色之外,其它性状完全一样。你伸手进去摸一把,摸到红球的概率是多少是可以推算出来的,这是“正向概率”;
如果我们事先并不知道袋子里面红球和白球的比例,而是闭着眼睛摸出一些球,然后根据手中红球和白球的比例,对袋子里红球和白球的比例作出推测,这就是“逆向概率”。
所以在逆向概率下,贝叶斯的底层逻辑就是:
如果能掌握一个事情的全部信息,当然能计算出一个客观概率(古典概率)。可是生活中绝大多数决策面临的信息都是不全的,我们手中只有有限的信息。
在这种情况下,贝叶斯定理能帮助我们在不知道事件正确概率的情况下做出合理的决策,并根据新信息不断调整概率分布,最终得出高概率的正确答案。
而从这个角度理解贝叶斯定理在ChatGPT中的应用:
P(B|A)/P(B)称为“可能性函数”,这是一个调整因子,也就是新信息B带来的调整,
于是,贝叶斯定理可以理解成下面的式子:后验概率(新信息出现后的A概率) = 先验概率(A概率) x 可能性函数(新信息带来的调整)
从而在ChatGPT对话系统中,如果把回答看作 A,已知的问题和信息看作 B,那么 ChatGPT 可以通过贝叶斯定理计算出 P(A|B),从而确定回答的概率。
即ChatGPT最朴素的技术原理来源于概率统计,通过贝叶斯定理, ChatGPT 可以计算出最优回复、实现交互。
也就难怪贝叶斯算法这一基于概率论的算法,成为机器学习中的重要理论支撑,在当下火热的人工智能领域起着基石的作用。
02
贝叶斯定理无处不在
好的公式,放之宇宙而皆准,贝叶斯公式正是如此。
到现在,贝叶斯式的智慧已经渗透到了人类社会的方方面面,涉及的领域包括但不限于:
医学诊断、遗传学、流行病学、天体物理学、生物学、政治、战争、密码学、地理学、神学、博弈、保险、赌博、决策、经济、航空航天工程、人工智能、神经科学、运动、心理学、考古学、古生物学、教育、社交网络、自动翻译、信号处理、基因组测序、蛋白质研究、资源分配、通信、图像分析、广告、金融、规划、物流以及许多其他领域……
它可以用于破译密码,寻找失事飞机,诊断疾病,搜索引擎,机器翻译,模式识别,研发新药,确定引起地震的断层,甚至可以用于宇宙学,研究哪一种宇宙模型最符合我们所在的宇宙。

用贝叶斯更新帮助搜索失踪飞机(《科学世界》2021年第6期)
而且随着大量数据输入模型进行迭代,随着计算能力不断提高,贝叶斯定理威力日益凸显。
贝叶斯,强大如斯,无处不在。
甚至影响我们的哲学思想,在贝叶斯主义者看来,没有任何关于现实世界的理论是终极真理,重要的是随着观测事实的积累,不断更新对理论的置信度。
可以说,贝叶斯派的智慧是一种关于偏见的智慧,在现实中,没有谁是全知全能的。
有的人因为害怕犯错而不再前进,有的人干脆否认偏见的普遍存在,把经过有限验证的道理当成普适真理。
而贝叶斯派则接受偏见的存在,他们相信,所谓追求真理,就是人们从偏见出发,一步步走向客观的过程。他们愿意以动态的视角看待真理,也愿意不断学习,不断走出偏见。

这一点,让我想到了《十三邀》贯穿数季的片头语关键词“偏见”。
无论是“我会带着我的偏见出发 等待这些偏见被打破或被再次印证”;
还是“我也好奇在时代浪潮之中一些崭新的创造力、想象力,正在被孕育,我会带着我的偏见与期待再次出发”;
亦或“只有更开放的对话、更多元的思考,才能追寻一种兼容之道,在宽阔的世界中,做一个不狭隘的人”;
它用语言这一符号,数次表达和传递着贝叶斯定理的智慧。
至此,我们或许有点明白为什么,比起要求高中生、甚至大学生掌握的许多其他数学概念来说:
贝叶斯公式似乎更容易学会,但它的深邃,远远超乎了我们的想象。
03
贝叶斯定理
数学之美的神秘面纱
从贝叶斯定理,我们可以看到数学最美妙的地方,正在于其复杂中的简单,简单中的复杂。
它的一行简单的公式,就能彻底改变我们所处的世界、以及看待世界的方式,这是一种独属于数学的浪漫与美感。
而且回看贝叶斯定理的发展,更是让人在AI技术凶猛的当下,拥有内心重获平静的力量。

《美丽心灵》
与其他统计学不同,贝叶斯定理是建立在主观判断的基础上,它需要有大量的样本数据,并在数据的基础上进行计算,数据量越大,计算结果越能反映现实世界。
在计算机诞生之前,这个前提条件是很难满足的,所以贝叶斯定理在历史上很长一段时间内都没有得到很好的应用,甚至一直被质疑。
直到互联网时代的来临,20世纪60年代,雷·所罗门诺夫将图灵的可计算性理论和贝叶斯公式结合起来,搭建了人工智能一般性框架的前身;
再到20世纪80年代,蒙特卡罗方法给贝叶斯公式的实际应用带来了革命,人们才逐渐发现贝叶斯定理超乎想象的强大。
英国数学家托马斯·贝叶斯在1763年首次提出贝叶斯定理之际,可能想不到:
他一个在当时看似普通、甚至被嗤之以鼻的发现,在260年后的今天,竟是ChatGPT的核心。
而这也正是数学的魅力之处,它支撑着我们继续前进,不仅不怕被AI取代,反而用AI探索更远的、像π一样无限的思想边界。

参考资料:
《贝叶斯的博弈:数学、思维与人工智能》
图灵教育:数学的极致:一个公式足以改变世界
图灵教育:被嫌弃的贝叶斯派的逆袭
量子学派:封杀这个公式,ChatGPT智商将为零
量子位:陶哲轩:ChatGPT已加入我的数学工作流

AI时代,掌握AI大模型第一手资讯!AI时代不落人后!
免费ChatGPT问答,办公、写作、生活好得力助手!
扫码右边公众号,驾驭AI生产力!




