文章主题：解一元二次方程, GPT, 求根公式, 技术含量
一，
这段时间大家都在谈论ChatGPT，而且是眼睁睁地看着ChatGPT颠覆了一个又一个领域。
如果到了某一天，这个世界上只剩下唯一一个领域尚未被ChatGPT颠覆的话，那么这个领域一定是————
数学！
所以，我们今天就来测试一下ChatGPT的数学水平。
二，
首先是一道解一元二次方程
GPT直接用求根公式了，这没什么技术含量，所以我要求，，，
看来一元二次方程难不倒它，那就试试一元三次方程
结果它居然用了牛顿迭代法！！
GPT在处理三次方程的根式求解问题时遇到了挑战，这并不令人意外，因为这个问题历史上曾让许多数学家感到困惑。然而，我们仍然有理由期待GPT在解决函数极值问题上表现出色，因为它在许多领域已经展现出了惊人的能力。
第一个极值问题GPT完整的解答了，所以我们决定加大难度
在上述内容中， calculus 符号的错误使用成为了显著的问题，并且由此引发了一系列的错误。这 type of mistake 揭示了 GPT 正在努力模拟人类的计算思维。当我指出了这个错误之后，它表现出了重新计算的能力。
这次没有计算错误，但是只求出一个极小值点，应该有无穷多个的。所以在函数极小值这种题目上GPT表现一般。
接下来，我们来看看GPT的数学证明水平，首先它很快就给出了根号3不是无理数的证明
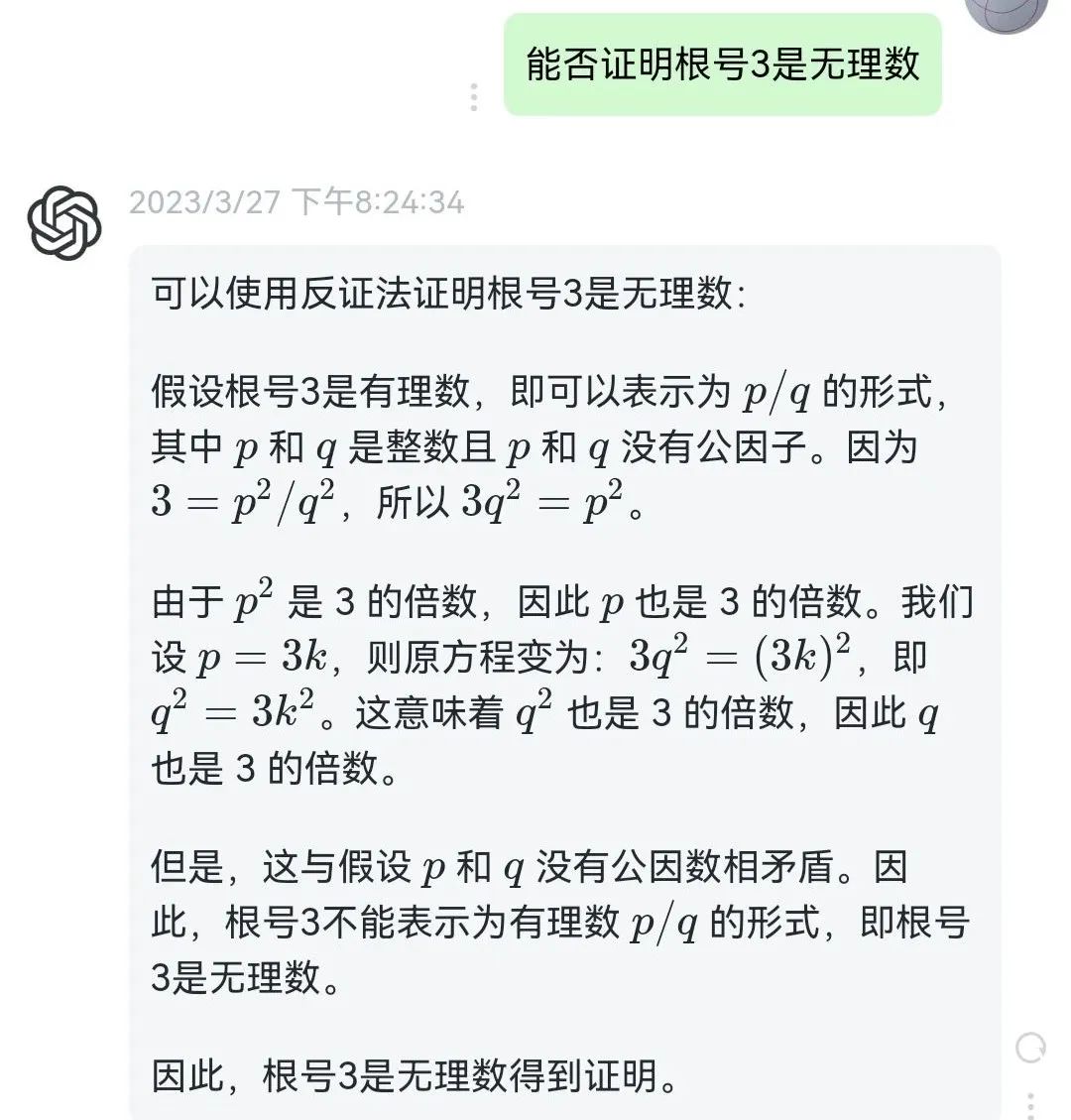
接下来要它证明根号12不是无理数，其实这只需注意到根号12是根号3的两倍即可。可惜GPT居然看不出这一点，而是直接照搬上面的证明，结果就闹笑话了。
最后我们来看看GPT会不会数学归纳法证明，
很快GPT就正确的运用数学归纳法给出了自然数平方和公式的证明，接下来看看它会不会运用归纳法证明算术基本定理，这个证明的难度增加了不少。
 fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
在第一部分中，GPT通过运用归纳法准确地论证了分解存在的可能性。然而，在进入第二部分，即分解唯一性的证明阶段时，GPT却采用了这样的结论：
“如果素数P整除一些正整数的乘积，则P必然会整除这个乘积的某个因子”
但是，这个结论本身是需要证明的，而且这个结论正是素数分解唯一性的直接推论，所以GPT的证明陷入了循环论证。
注意，这个错误也是许多学数论的学生甚至老师经常会犯的错误，这又一次说明了GPT正是在极力模仿人类的思维模式，这很可怕！！
根据以上上的测试，我认为这个GPT的数学水平差不多只在高中水平。
GPT-4 目前是最强大的人工智能模型之一，但它在我国的直接使用仍受到限制。一旦未来我国对此进行了评估并获得了许可，我将精心设计一套高难度的数学测试来评估 GPT-4 的数学能力，并期待您的关注与参与。
[投稿须知】公众号《许兴华数学》诚邀全国各地中小学数学教师、教研员和数学爱好者热情投稿！来稿时请注意以下五点：
（1）来稿请注明真实姓名、工作单位、联系方式（无具体工作单位和真实姓名的投稿，一般都不会采用）。（2）来稿一般要求同时用word文档和PDF格式的电子稿件（防止不同版本的Word打开时出现乱码）。另外，也接受少数著名教师的手写稿（手写稿必须清晰可读）。
（3）每篇文章请认真审查复核，防止错误发生，来稿文责自负。如有抄袭，则有可能被举报并受到有关著作版权部门的追责。
（4）投稿邮箱：chinamatha@163.com；或加主编微信xuxinghua168投稿（加时请注明：投稿）.
（5）本公众号对优秀作者和名师一般会附上“作者简介”，以让广大读者更好地了解作者的研究成果和方向，以便进一步学习作者的相关数学思想或解题方法。
【推荐阅读】
李鸿昌杨春波等：圆锥曲线中的定点问题.新高考版《高中数学一点一题型》新书预读.（许兴华数学）
2022年中国数学奥林匹克希望联盟夏令营试题（二）及参考答案
【解题研究】用“对数单身狗，指数找基友”研究高考导数难题（之二）
2022年高考全国卷命题基本原则和总体思路（附九科全国卷试题评析）
【教育博览】尖子生的秘密：连晚上学习都是有套路的！很实用，转给孩子吧！
【高考研究】2021年高考数学很有可能要考的80道题! 认真看了才知道命题有这些规律…
公众号《许兴华数学》近年（2018~2021年）“高考研究”与“数学解题”优秀文章136篇选读
【春节快乐】适合教师在假期观看的十部电影（内有视频，点击可看）
AI时代，拥有个人微信机器人AI助手！AI时代不落人后！
免费ChatGPT问答，办公、写作、生活好得力助手！
搜索微信号aigc666aigc999或上边扫码，即可拥有个人AI助手！
